Matriks: Perkalian Matriks Dengan Sebuah Skalar

Skalar adalah sebuah bilangan yang dikalikan dengan sebuah matriks. Selanjutnya, skalar tersebut akan kita kalikan dengan setiap elemen di dalam matriks.

(a) Menghitung 3A.

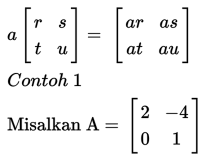
Dalam contoh ini, 3 adalah skalar. Skalar ini, kemudian akan dikalikan dengan setiap elemen di dalam matriks A, sehingga diperoleh :

(b) Menghitung ½ A.

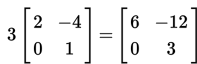
 Dalam contoh ini, ½ adalah skalar. Skalar ini, kemudian akan dikalikan dengan setiap elemen di dalam matriks A, sehingga diperoleh :

Perhatikan bahwa dimensi (ukuran) matriks tidak berubah ketika kita mengalikannya dengan suatu skalar.

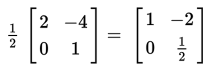
Sifat-sifat perkalian skalar

Misalkan A dan B adalah matriks berukuran m x n dan misalkan  c dan d adalah skalar. Sifat-sifat berikut ini berlaku dalam perkalian skalar :

Sifat tertutup : cA merupakan matriks berukuran m x n
Sifat asosiatif: (cd)A = c(dA)
Sifat distributif : c(A + B) = cA + cB  dan  (c + d)A = cA + dA
Sifat komutatif : gA = Ag
Sifat identitas perkalian : 1 • A = A
Sifat perkalian dengan nol : 0 • A = O dan cO = O, dimana O adalah matriks nol 
Contoh 2

 

Perhatikan bahwa dalam contoh di atas, terdapat 2 buah skalar : -2 dan 3.

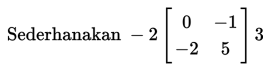
Karena perkalian skalar bersifat asosiatif, maka kita dapat mengelompokkan ketiga bagian tersebut menjadi sebarang kelompok. Selanjutnya, karena perkalian skalar bersifat komutatif, maka kita dapat menyusun urutan dari ketiga bagian tersebut secara acak. Dalam hal ini, kita akan mengalikan kedua skalar terlebih dahulu, kemudian kita akan mengalikan hasilnya dengan matriks di atas.

Contoh 3

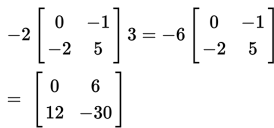
Toko Pizza milik Luka menawarkan pilihan menu sebagai berikut :

                                        Kecil     Besar
Cheese Pizza                      $4.25     $7.25
Mushroom Pizza                   $5.00     $8.25
Pepperoni Pizza                   $5.45     $8.95

Karena biaya persediaan meningkat, Luka memutuskan untuk menaikkan harga sebesar 20%. Berapakah harga pizza yang baru?
Untuk menambahkan kenaikan harga sebesar 20% kedalam harga asli, kita dapat mengalikan harga asli dengan 1,2. Dengan demikian, diperoleh model perkalian skalar sebagai berikut :

Harga pizza yang baru adalah :
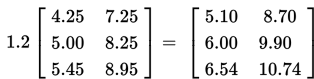
                                                Kecil     Besar
Cheese Pizza                              $5.10     $8.70
Mushroom Pizza                          $6.00     $9.90
Pepperoni Pizza                          $6.54     $10.74

Contoh 4

Contoh 5

Matriks juga dapat digunakan untuk merepresentasikan bentuk dalam bidang koordinat. Sebagai contoh, jika diberikan sebuah segitiga dengan ketiga titik berada pada koordinat (0, -1), (2, 3), dan (-1, 5), maka matriks yang terbentuk adalah sebagai berikut :

Perkalian dengan suatu skalar akan dapat memperbesar maupun memperkecil ukuran dari bentuk geometri. Proses ini disebut dengan dilatasi. Jika dilakukan perkalian dengan suatu bilangan yang lebih besar dari 1, maka ukuran akan membesar dan jika dilakukan perkalian dengan bilangan pecahan atau bilangan desimal di antara 0 dan 1, maka ukuran akan mengecil.

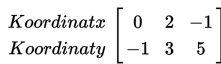
Selanjutnya, untuk memperbesar ukuran segitiga menjadi dua kali, kita dapat mengalikan matriks yang terbentuk dengan skalar 2.
Dengan demikian, diperoleh :

Jadi, koordinat segitiga yang baru adalah : (0, -2), (4, 6), and (-2, 10).

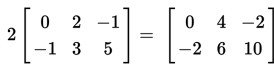
Untuk mengecek hasil yang telah kita peroleh, kita dapat menggambar kedua segitiga : segitiga asli dan segitiga yang baru dalam bidang koordinat. Jika hasil yang diperoleh benar, maka kedua segitiga itu akan nampak proporsional, hanya saja ukurannya berbeda.