Beberapa waktu yang lalu kalian telah mempelajari materi tentang hubungan antara titik, garis dan bidang, dan sekarang kalian akan mempelajari tentang jarak antara titik, garis dan bidang.
Untuk mengawali materi tentang menghitung jarak, mari kita mulai dengan topik jarak antara dua titik.
1. Jarak antara dua titik adalah panjang ruas garis yang menghubungkan kedua titik tersebut.
d adalah jarak antara titik A dan B
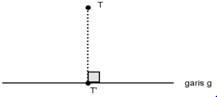
2. Proyeksi sebuah titik T pada sebuah garis g dapat diperoleh dengan cara menarik garis tegak lurus dari titik T terhadap garis g. Selanjutnya, perpotongan antara garis tegak lurus dari titik T dengan garis g yaitu titik T' , disebut proyeksi titik T pada garis g.
3. Proyeksi sebuah titik P pada bidang V dapat diperoleh dengan cara menarik garis tegak lurus dari T ke bidang V. Perpotongan antara garis lurus dari T dengan bidang V, yaitu titik P' disebut sebagai proyeksi titik P pada bidang V.
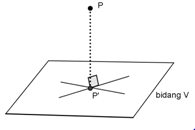P' adalah proyeksi P pada bidang V.
4. Untuk menghitung jarak antara dua titik diperlukan pertolongan segitiga siku-siku, kemudian digunakan rumus teorema Pythagoras.
Untuk lebih jelasnya, mari kita perhatikan contoh berikut.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung jarak
a) titik A dan titik C
b) titik B dan titik H
c) titik E dan titik P (titik P adalah perpotongan diagonal bidang sisi BG dan CF)
d) titik L ke titik G (titik L adalah proyeksi titik C pada bidang BDG)
Jawab :
a)
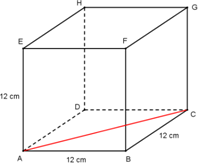
Untuk menghitung jarak titik A dan C, maka dibuat ∆ABC dengan siku-siku di B, kemudian dengan menggunakan teorema Phytagoras diperoleh :
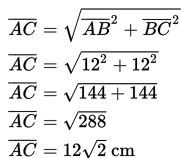
(untuk menghitung panjang diagonal bidang sisi kubus dengan rusuk a dapat juga digunakan rumus a√2).
b)
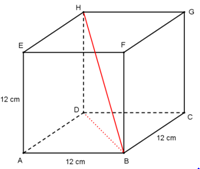
Untuk menghitung jarak titik B dan H digunakan pertolongan ∆DBH (segitiga siku-siku di D), kemudian baru digunakan rumus teorema Pythagoras.
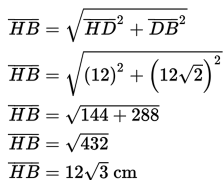
(untuk menghitung panjang diagonal ruang kubus dengan rusuk a dapat juga digunakan rumus a√3).
c)
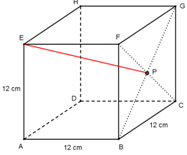
Untuk menghitung jarak titik E dan P digunakan pertolongan ∆EFP (segitiga siku-siku di F), kemudian baru digunakan rumus teorema Pythagoras.
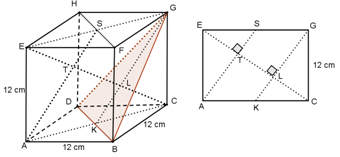
Proyeksi titik C pada bidang BDG adalah titik L.
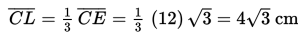Karena ∆GLC siku-siku di L, maka dengan teorema Phytagoras diperoleh :
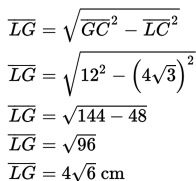
Untuk mengawali materi tentang menghitung jarak, mari kita mulai dengan topik jarak antara dua titik.
1. Jarak antara dua titik adalah panjang ruas garis yang menghubungkan kedua titik tersebut.
2. Proyeksi sebuah titik T pada sebuah garis g dapat diperoleh dengan cara menarik garis tegak lurus dari titik T terhadap garis g. Selanjutnya, perpotongan antara garis tegak lurus dari titik T dengan garis g yaitu titik T' , disebut proyeksi titik T pada garis g.
4. Untuk menghitung jarak antara dua titik diperlukan pertolongan segitiga siku-siku, kemudian digunakan rumus teorema Pythagoras.
Untuk lebih jelasnya, mari kita perhatikan contoh berikut.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung jarak
a) titik A dan titik C
b) titik B dan titik H
c) titik E dan titik P (titik P adalah perpotongan diagonal bidang sisi BG dan CF)
d) titik L ke titik G (titik L adalah proyeksi titik C pada bidang BDG)
Jawab :
a)
Untuk menghitung jarak titik A dan C, maka dibuat ∆ABC dengan siku-siku di B, kemudian dengan menggunakan teorema Phytagoras diperoleh :
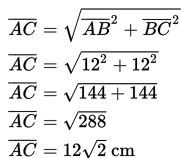
(untuk menghitung panjang diagonal bidang sisi kubus dengan rusuk a dapat juga digunakan rumus a√2).
b)
Untuk menghitung jarak titik B dan H digunakan pertolongan ∆DBH (segitiga siku-siku di D), kemudian baru digunakan rumus teorema Pythagoras.
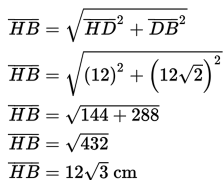
(untuk menghitung panjang diagonal ruang kubus dengan rusuk a dapat juga digunakan rumus a√3).
c)
Untuk menghitung jarak titik E dan P digunakan pertolongan ∆EFP (segitiga siku-siku di F), kemudian baru digunakan rumus teorema Pythagoras.
Proyeksi titik C pada bidang BDG adalah titik L.
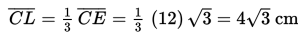
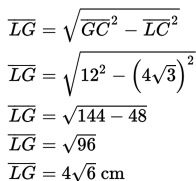
0 komentar:
Post a Comment